2D Model – Ham et al. (2004)

This 2D model, based on Ham et al. (2004), provides an estimate of a steady-state plume length ($L_{max}$ ) and explores the effects of longitudinal and transverse dispersivity on the steady state plume length.

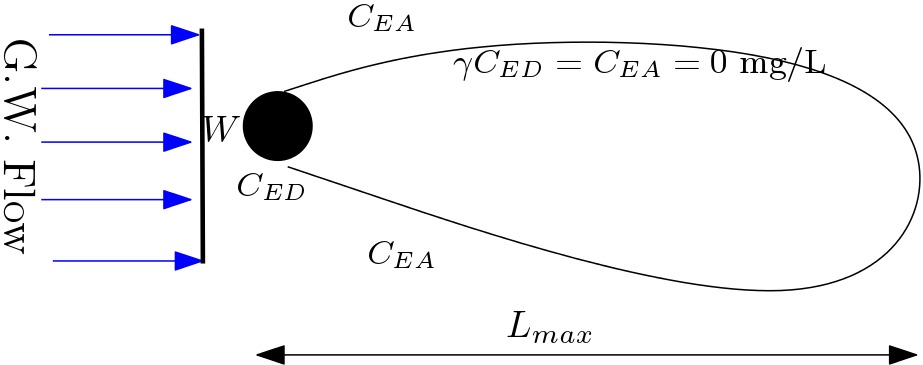
Output from Ham et al.(2004) model

Ham et al.(2004) provides the following explicit expression for $L_{max}$:

$$ L_{max} = \frac{W^2}{4 \pi\alpha_{TH}}{\bigg(\frac{ \gamma C_{ED}^\circ }{ C_{EA}^\circ}\bigg)^2} $$

in which:

$W$ = Width of contaminated source [L]
$\alpha_{TH}$ = horizontal transverse dispersivity [L]
$C_{ED}^\circ$ = Contaminant (Electron Donor) concentration [ML$^{-1}$]
$C_{EA}^\circ$ = Partner Reactant (Electron Acceptor) concentration [ML$^{-1}$]

The model is based on the following assumptions:

  1. A point source with constant mass flow injection.
  2. An instantaneous reaction between an injected compound and a reactant in the ambient groundwater at the plume fringe.

Reference: Ham, P.A.S., Schotting, R.J., Prommer, H., Davis, G.B., 2004. Effects of hydrodynamic dispersion on plume lengths for instantaneous bimolecular reactions. Adv. Water Resour. 27, 803–813. https://doi.org/10.1016/j.advwatres.2004.05.008