3D Model – Liedl et al. (2011)¶
This model, based on Liedl et al. (2011), provides an estimate of a steady-state plume length ($L_{max}$ ) from a 3D model domain (see figure). This model extends the 2D model present in Liedl et al. (2005). As is in the 2D model, in this model too the vertical orientation refers to $z$-axis being aligned to the aquifer thickness. The domain width and length is infinite in this model.
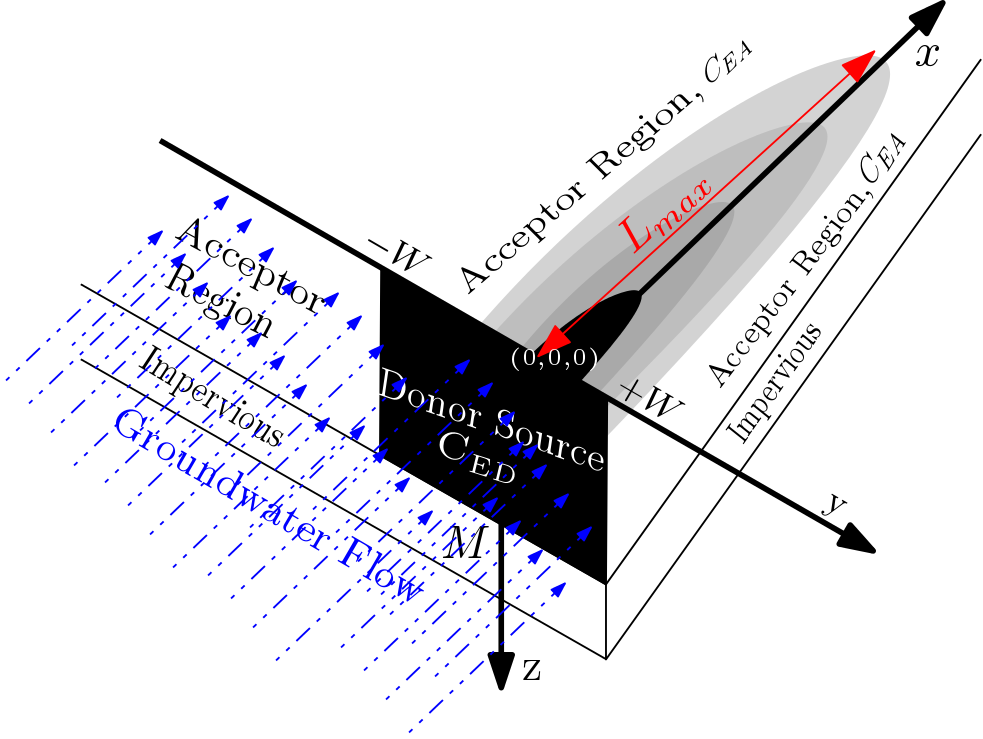
Liedl et al.(2011) provides the following explicit expression for $L_{max}$:
$$ \text{erf}\bigg(\frac{W}{\sqrt{4\alpha_{Th}L}}\bigg)\,\text{e}^{-\alpha_{Tv}L \big(\frac{\pi}{2M}\big)^2} =\frac{\pi}{4}\frac{\gamma C_{Thres}+C_{EA}^\circ}{\gamma C_{ED}^\circ+C_{EA}^\circ} $$in which:
$M$ = Source Thickness [L], which is equal to Aquifer thickness ($A_t$) [L]
$\alpha_{Tv}$ = Vertical Transverse Dispersivity [L]
$W$ = Source Width [L]
$\alpha_{Th}$ = Horizontal Transverse Dispersivity [L]
$\gamma$ = Reaction stoichiometric ratio [ ]
$C_{ED}^\circ$ = Contaminant (Electron Donor) concentration [ML$^{-1}$]
$C_{EA}^\circ$ = Partner Reactant (Electron Acceptor) concentration [ML$^{-1}$]
$C_{Thres}$ = Threshold Contaminant Concentration [ML$^{-1}$]
The $C_{Thres}$ in this model allows to set the contaminant concentration to any value greater than or equal to zero, and then $L_{max}$ is length from the origin to that maximum distance of $C_{Thres}$ along $x$-axis .
The model is based on the following assumptions:
- Steady-state condition in a homogeneous and isotropic aquifer.
- A single step bi-molecular instantaneous reaction between reactants taking place only at the fringe.
- The contaminant source (Electron Donor) penetrates entire thickness of the aquifer.
Reference:
Liedl, R., Yadav, P.K., Dietrich, P., 2011. Length of 3-D mixing-controlled plumes for a fully penetrating contaminant source with finite width. Water Resour. Res. 47. https://doi.org/10.1029/2010WR009710