BIOSCREEN–AT – Karanovic et al. (2007)¶
The model provides a three-dimensional solution for transport of dissolved contaminants, incorporating natural attenuation processes. As shown in Figure 1, the source is given as a patch specified-concentration boundary condition.
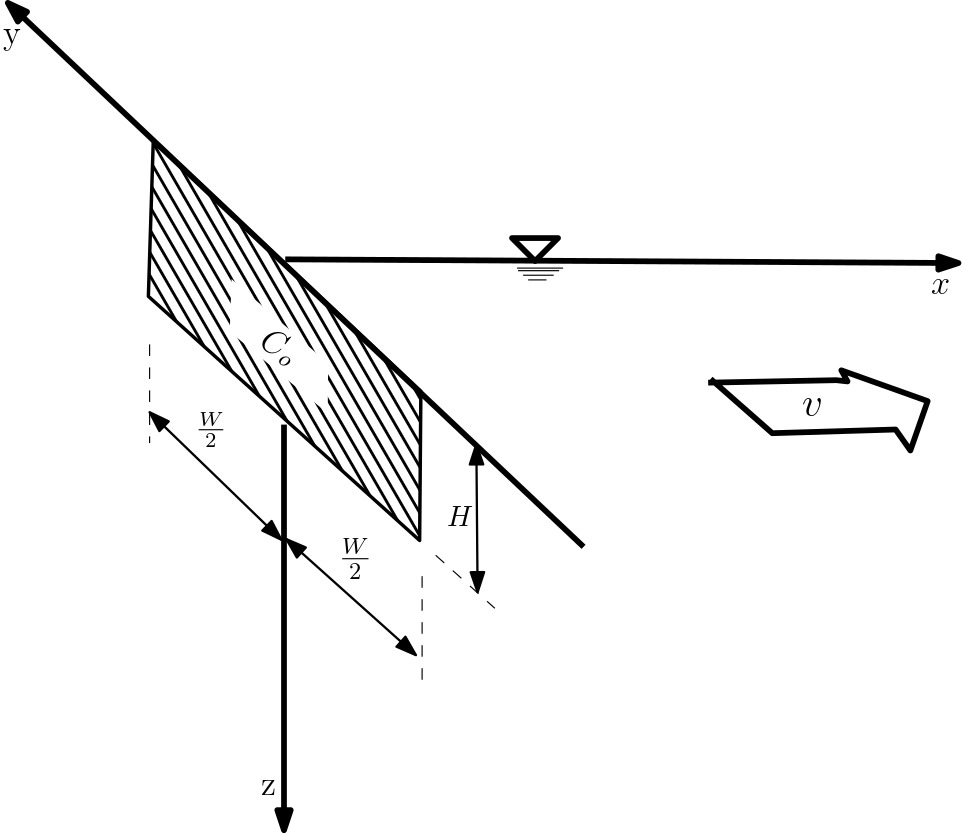
Figure 1: Conceptual Model
Newell et al. (1997)/ Karanovic et al. (2007) Provide the following expression for an exact analytical solution:
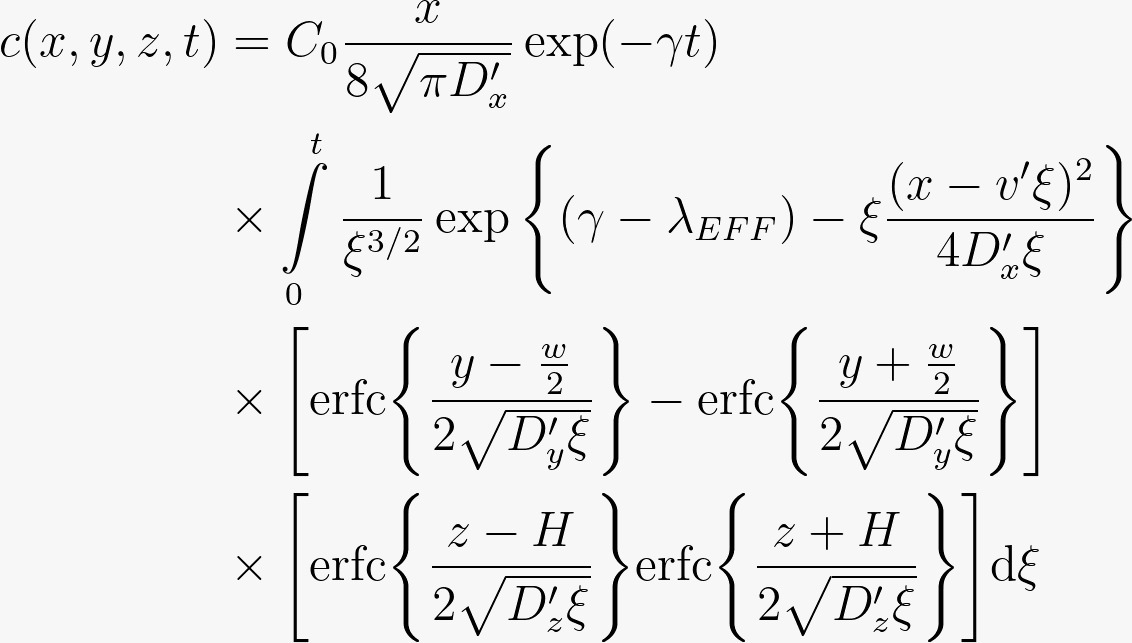
with:
$c_{o}$ = initial source concentration
$D_{x}^{'}$ = dispersion coefficient divided by retardation factor Dx/R
$D_{y}^{'}$ = dispersion coefficient divided by retardation factor Dy/R
$D_{z}^{'}$ = dispersion coefficient divided by retardation factor Dz/R
$\gamma$ = source decay coefficient
$\lambda_{eff}$ = effective first order decay coefficient
The model is based on the following assumptions:
- Aquifer extends semi-infinite in x-direction, infinite in y-direction and extends from water table to relatively large depth.
- Groundwater flow is steady and one dimensional.
- The solute undergoes equilibrium sorption and first-order transformation reactions.
- The aquifer is homogeneous and Lmax is always found on the center line.
The CAST Project acquires the maximum plume length Lmax from this model, using Gauss-Legendre-Quadrature to obtain a solution. Figure 2 shows the concentration of the contaminant along x-direction.
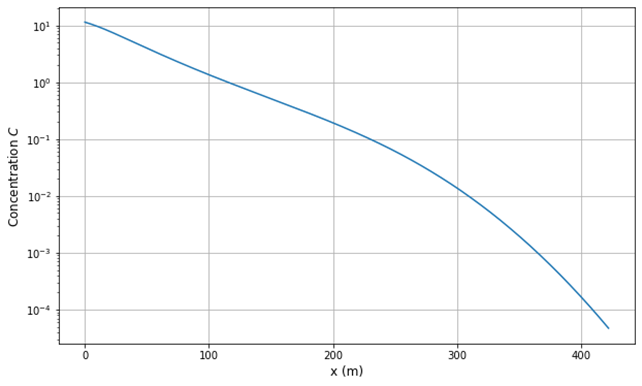
Figure 2: Concentration along center line
Reference:
Marinko Karanovic, Christopher J. Neville, and Charles B. Andrews. BIOSCREEN-AT: BIOSCREEN with an Exact Analytical Solution. Vol. 45, No. 2 GROUND WATER March–April 2007 (pages 242–245).
S.S. Papadopulos & Associates, Inc. , https://www.sspa.com/software/bioscreen